Dissertation

Abstract

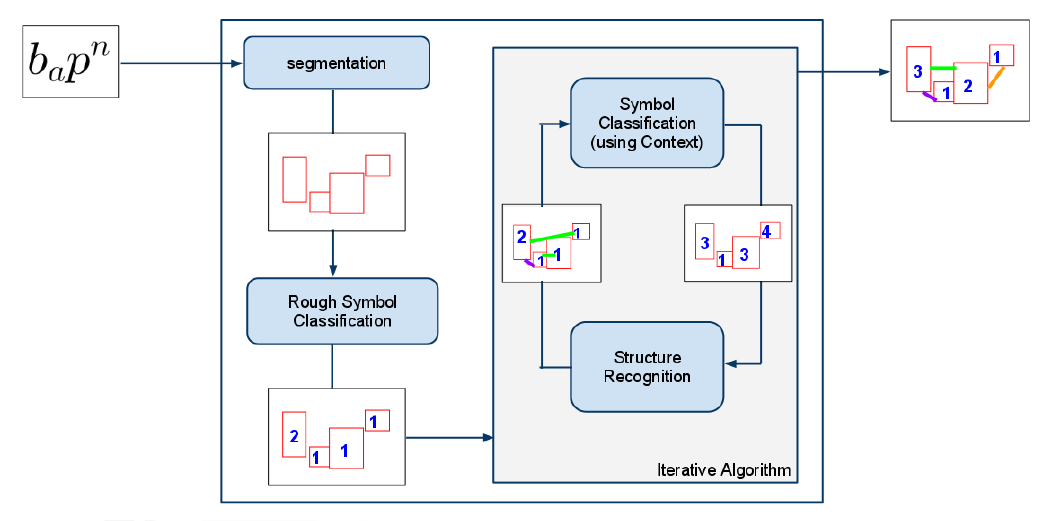
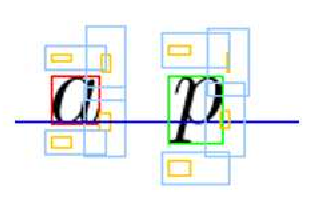
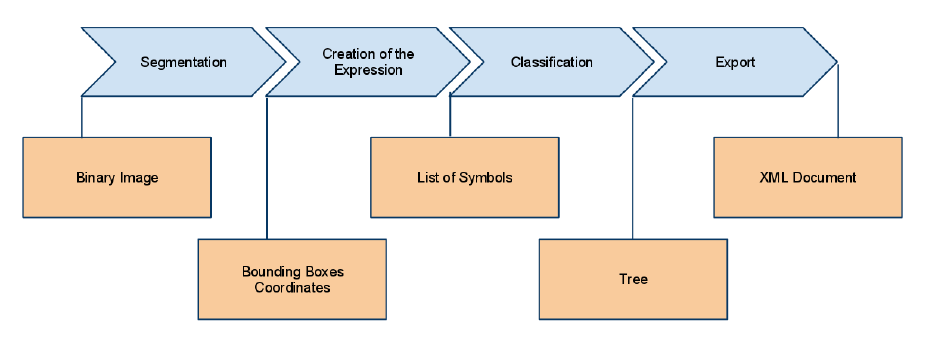
Unlike texts, printed mathematical expressions have a two-dimensional nature, and their recognition involves the recognition of the structure of the formula and of the symbols contained in it. In most research, the structure recognition uses the identity of symbols. Moreover, a few previous works use the structure in the symbol recognition, or machine learning techniques in the structure recognition part. There is a lot of mathematical symbols, they can be very similar, and new symbols are being invented by scientists. The arrangements of symbols, however, evolve less. In this dissertation, we investigate the possibility of recognizing the structure of the mathematical expression without the symbols' identity. We also perform a prior classification of the symbols using the structure only. Moreover, we use very few knowledge about mathematical expression syntax. This approach has, to the best of our knowledge, never been tried. We built a system using machine learning techniques, such as neural networks and fuzzy logic. A binary image representing a mathematical expression is segmented, and the recognition is performed using the symbols' bounding boxes. An iterative algorithm using a multi-classifier system recognizes the structure and classifies the symbols. The results proved that the context of a symbol, when known and used, can help classify the symbol. The structure recognition using a non-recursive algorithm with very few backtracking yielded good results. This project proved that the symbols' identity is not essential for the structure analysis. Moreover, the structure recognition provides some useful information for the symbol classification. This classification is assumed to help the symbol recognition in a future work. Finally, the machine learning approach produced a flexible system, able to adapt to unknown symbols and writing styles, and to return confidence values for the recognition, rather than a crisp interpretation.

Keywords

machine learning mathematical formula recognition mathematical structure recognition neural network MLP fuzzy logic

Electronic version

MSc Dissertation : "Mathematical Formula Recognition using Machine Learning Techniques"
Presentation slides (in French)

About

Context

This work was submitted for the completion of the MSc in Computer Science of Oxford University. The MSc is a one-year program divided in three parts. Courses take place in the first two terms of eight weeks. I attended mainly courses on artificial intelligence. The last part is a research project, carried out for five months. I chose the topic and had the privilege to work under Dr. Vasile Palade supervision.

Motivation

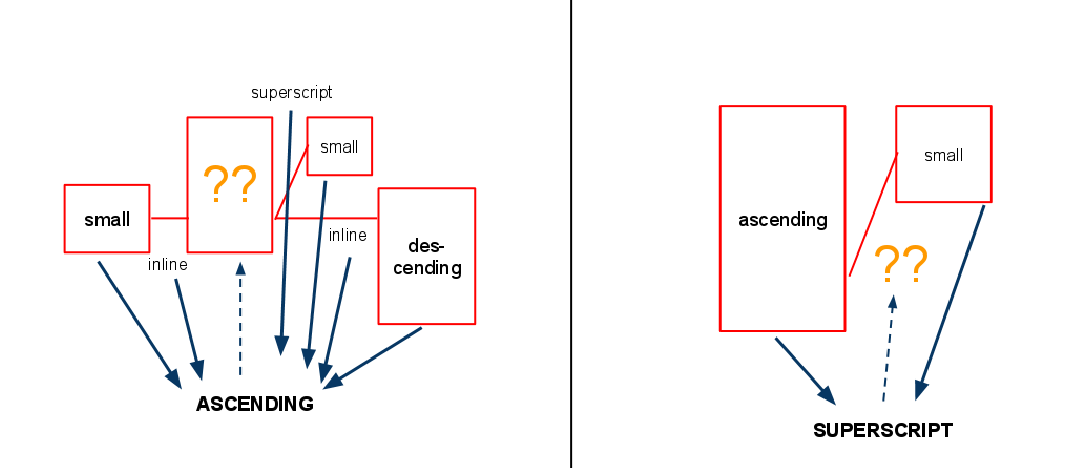
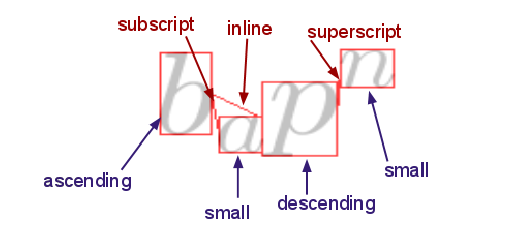
Mathematical symbol recognition is a difficult task, because lots of symbols look similar and new symbols can be invented. My hypothesis was that symbol recognition is not necessary to perform the recognition of the structure. The structure can in turn help symbol classification, giving an a priori knowledge about the symbols' identities. In this work, I investigate to which extent it is possible to recognize simple mathematical expressions' structure with a limited knowledge about the symbols themeselves. In an iterative process, I classify the symbols and analyze the structure.

Acknowledgements

I am grateful to my supervisor, Dr. Vasile Palade, for his valuable comments, his support and our interesting discussions.